复习——数学篇

线性代数

行列式

1、行列式性质及计算

①互换行（列），变号：交换行列式的两行（列），行列式的值变号。比如$D=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}$ ，交换两行得$\begin{vmatrix}a_{21}&a_{22}\\a_{11}&a_{12}\end{vmatrix}=-D$ 。

②提公因子：行列式某一行（列）的所有元素都有公因子$k$ ，可把$k$提到行列式外面。即若$D=\begin{vmatrix}ka_{11}&ka_{12}\\a_{21}&a_{22}\end{vmatrix}$ ，则$D = k\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}$ 。

③倍加：把行列式某一行（列）的元素乘以数$k$后加到另一行（列）对应元素上，行列式的值不变。比如$D=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}$ ，第一行乘$k$加到第二行，得$\begin{vmatrix}a_{11}&a_{12}\\a_{21}+ka_{11}&a_{22}+ka_{12}\end{vmatrix}=D$ 。

④拆分：若行列式某一行（列）的元素都是两数之和，可拆成两个行列式之和。如$D=\begin{vmatrix}a_{11}+b_{11}&a_{12}+b_{12}\\a_{21}&a_{22}\end{vmatrix}$ ，则$D=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}+\begin{vmatrix}b_{11}&b_{12}\\a_{21}&a_{22}\end{vmatrix}$ 。

⑤对应成比例，值为零：若行列式有两行（列）对应元素成比例，行列式的值为$0$ 。比如$D=\begin{vmatrix}a_{11}&a_{12}\\ka_{11}&ka_{12}\end{vmatrix}$ ，两行成比例，$D = 0$ 。

2、行列式展开、范德蒙行列式

定义

• 余子式 $\boldsymbol{M_{ij}}$：去掉行列式中元素 $\boldsymbol{a_{ij}}$ 所在的第 $\boldsymbol{i}$ 行和第 $\boldsymbol{j}$ 列，剩余元素构成的新行列式。
• 代数余子式 $\boldsymbol{A_{ij}}$：$\boldsymbol{A_{ij}=(-1)^{i+j}M_{ij}}$ （符号由元素位置的行标 $\boldsymbol{i}$、列标 $\boldsymbol{j}$ 决定 ）

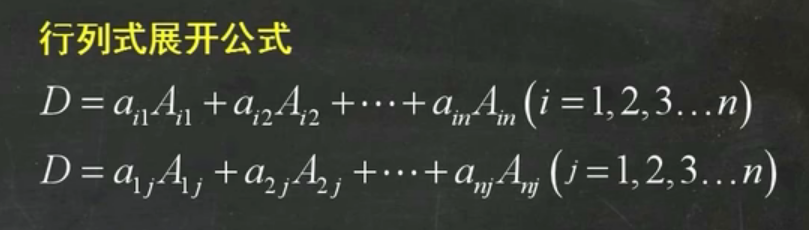
按行展开 对 $n$ 阶行列式 $D$，取第 $\boldsymbol{i}$ 行（$i = 1,2,\dots,n$ ），有： $\boldsymbol{D = a_{i1}A_{i1} + a_{i2}A_{i2} + \cdots + a_{in}A_{in}}$ 其中，$\boldsymbol{a_{ij}}$ 是行列式第 $i$ 行第 $j$ 列的元素，$\boldsymbol{A_{ij}}$ 是 $\boldsymbol{a_{ij}}$ 的代数余子式（$A_{ij}=(-1)^{i+j}M_{ij}$ ，$M_{ij}$ 为余子式 ）。

按列展开 对 $n$ 阶行列式 $D$，取第 $\boldsymbol{j}$ 列（$j = 1,2,\dots,n$ ），有： $\boldsymbol{D = a_{1j}A_{1j} + a_{2j}A_{2j} + \cdots + a_{nj}A_{nj}}$ 同理，$\boldsymbol{a_{ij}}$ 是行列式第 $i$ 行第 $j$ 列的元素，$\boldsymbol{A_{ij}}$ 是对应代数余子式 。

矩阵

1、矩阵的三则运算

行列式 $D=\begin{vmatrix}1&2&3\\1&3&4\\3&1&2\end{vmatrix}$ ，矩阵$A=\begin{pmatrix}1&2&3\\1&3&4\\3&1&2\end{pmatrix}$ ；

①行列式是一个数，矩阵是一个表

②行列式是 $n×n$ 阶，矩阵是 $n×m$ 阶（$n$ 和 $m$ 可以不相等也可以相等）

③ $\lambda\vert A\vert$ 是把行列式某行（列）乘以 $\lambda$ ；$\lambda A$ 是把矩阵里每个元素都乘以 $\lambda$

④行列式加减是数的运算；矩阵的加减只能是同型矩阵，对应元素的加减

⑤矩阵如果是方阵（$n = m$ ）的时，有行列式值

矩阵的乘法:$AB \neq BA$

2、转置矩阵、伴随矩阵、单位矩阵、逆矩阵

1）转置矩阵 ($A^{\text{T}}$ )

就是行变列、列变行

$\boldsymbol{ A=\begin{pmatrix}1&2&3\\1&3&4\\3&1&2\end{pmatrix},\quad A^{\text{T}}=\begin{pmatrix}1&1&3\\2&3&1\\3&4&2\end{pmatrix} }$

2）伴随矩阵 $A^{*}=\begin{pmatrix}A_{11}&A_{21}&\cdots&A_{n1}\\A_{12}&A_{22}&\cdots&A_{n2}\\\vdots&\vdots&\ddots&\vdots\\A_{1n}&A_{2n}&\cdots&A_{nn}\end{pmatrix}$

3）单位矩阵 E： $E = \begin{pmatrix}1&0\\0&1\end{pmatrix}$ $E = \begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}$ $|E| = 1$ $EA = AE = A$

4）逆矩阵 $A^{-1}$

$AB = BA = E$则$B$为$A$得逆矩阵，记$B = A^{-1}$；即： $AA^{-1} = E$ 公式： $A^{-1} = \frac{A^{*}}{\vert A \vert}$ 可逆得充要条件$\vert A \vert \neq 0$

3、矩阵的行列式运算

一些重要的运算性质:$|kA| = k^n|A|$ 、 $|A^{-1}| = \frac{1}{|A|}$、 $(kA)^{-1} = \frac{1}{k}A^{-1}$ 、 $|A^{*}| = |A|^{n - 1}$ 、 $A^{*} = |A|A^{-1}$、 $|AB| = |BA| = |A||B|$

初等行变换

1、初等行变换

①换行 ②倍乘 ③倍加 三种运算

变换用箭头连接而非等号，换行后，矩阵前不会加负号。

倍乘时，也并不会在前面提出一个系数。

阶梯形矩阵的特征 1. 若有全零行，则全零行位于最下方 2. 每个阶梯首项为主元，主元依次往右 3. 阶梯形不唯一

最简形 ①主元为1 ②主元所在列的其他元素都为0 ③最简形是唯一

2、求逆矩阵

题1. 若 $A = \begin{pmatrix}1&1&-1\\2&1&0\\1&-1&0\end{pmatrix}$ ，求 $A^{-1}$ 。$(A\vdots E)\longrightarrow(E\vdots A^{-1})$ 只需将A通过初等行变换，变为单位矩阵$E$，则右边的矩阵就是$A^{-1}$

题2. 若$A = \begin{pmatrix} 1 & 3 \\ 2 & 2 \end{pmatrix}$ 求$A^{-1}$

$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \quad$ $A^{-1}$ = $\frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$ 主对调，次反号，除以值

题3. 设 $A = \begin{pmatrix} 4 & 2 & 3 \\ 1 & 1 & 0 \\ -1 & 2 & 3 \end{pmatrix}$，且 $AX = A + 2X$，求 $X$ 解：$AX = A + 2X \Rightarrow AX - 2X = A \Rightarrow (A - 2E)X = A$

通过像题1，将$(A - 2E)$化为单位矩阵，则右边的矩阵即为$X$

矩阵的秩

k 阶子式：在一个矩阵或行列式中取k行k列，交叉处的k²个元素按原顺序构成的行列式。

1 从子式的角度定义：矩阵的秩就是矩阵中非零子式的最高阶数。

2 从极大线性无关组的角度定义：矩阵的所有行向量中极大线性无关组的元素个数。

3 从标准型的角度定义：求一个矩阵的秩，可以先将其化为行阶梯型，非零行的个数即为矩阵的秩。

矩阵的秩即为主元的个数

秩的性质如下：

1. $A_{m \times n} \quad R(A) \leq \min\{m, n\}$
2. $A$ 为方阵 $R(A) = n \Leftrightarrow |A| \neq 0 \quad R(A) < n \Leftrightarrow |A| = 0$
3. $R(A^T) = R(A) = R(kA) \quad (k \neq 0)$
4. $R(AB) \leq R(A) \quad R(AB) \leq R(B)$

向量

1、向量组

向量组：由若干个向量组成的集合，通常记为 ${v_1, v_2, \dots, v_n}$。

2、线性相关

① 存在一组不全为0的数 ( $k_1, k_2, \cdots k_m$ )，使$k_1a_1 + k_2a_2 + \cdots + k_ma_m = 0$则称向量组$a_1, a_2, \cdots a_m$ 线性相关，否则线性无关。

② 若$R(a_1, a_2, \cdots a_m) < m$，则向量线性相关若$R(a_1, a_2, \cdots a_m) = m$，则向量线性无关。

③ 极大无关组

阶梯型矩阵最简形的主元所在列是极大无关组

解方程组

1、齐次线性方程组

方程右边全为0，称为齐次线性方程组。求解一般分为三步:判断解的情况、求解向量、表示通解

先写出系数矩阵，然后将其化简为最简形的阶梯矩阵。

判定：系数矩阵$A$

$R(A) = n$只有零解

$R(A) < n$有无穷多解且有 $n - R(A)$个解向量

通解即通过系数将解向量连接起来

1、自由变量不能全为零 2、不同的解向量线性无关

2、非齐次线性方程组 $Ax = \beta$

题2. 求非齐次线性方程组$\begin{cases} x_1 + x_2 - x_3 - x_4 = 1 \\ 2x_1 + x_2 + x_3 + x_4 = 4 \\ 4x_1 + 3x_2 - x_3 - x_4 = 6 \\ x_1 + 2x_2 - 4x_3 - 4x_4 = -1 \end{cases}$ 的解。

写出增广矩阵$(A:\beta)$，并进行初等行变换

1. 无解

$R(A) \neq R(A:\beta)$

1. 有唯一解

$R(A) = R(A:\beta) = n$

1. 有无穷多解

$R(A) = R(A:\beta) < n$

• $A$ 是系数矩阵
• $(A:\beta)$ 是增广矩阵
• $R(\cdot)$ 表示矩阵的秩
• $n$ 是未知数的个数

非齐次方程通解$X$ $X=$(齐次通解+非齐次特解)

特征值、特征向量、对角化

1、求特征值、特征向量

• 给定方阵 $A \in \mathbb{R}^{n \times n}$。
• 如果存在标量 $\lambda \in \mathbb{R}$，和非零向量 $x \in \mathbb{R}^n$，使得：

则称：

• $\lambda$ 是矩阵 $A$ 的特征值 (eigenvalue)，
• $x$ 是对应的特征向量 (eigenvector)。

题目：求矩阵$A = \begin{pmatrix} 3 & -1 \\ -1 & 3 \end{pmatrix}$的特征值 即求解$|A−λE|=0⇒λ$ 得到的$\lambda$即特征值。

求特征向量即$(A−λ_{i}E)x=0$的基础解系

2、相似对角化

若方阵 $A \in \mathbb{R}^{n \times n}$，存在可逆矩阵 $P$，使得

其中 $D$ 是对角矩阵，则称 $A$ 与 $D$ 相似，称 $A$ 可相似对角化。

解题方法：

①求特征值($\lambda_1,\lambda_2,\cdots,\lambda_m$) ②求基础解系($a_1,a_2\cdots a_m$) ③($P=(a_1,a_2\cdots a_m$)) $P^{-1}AP=\begin{pmatrix}\lambda_1&&&\\&\lambda_2&&\\&&\ddots&\\&&&\lambda_m\end{pmatrix}$

相似对角化的条件:

一个 $n$ 阶矩阵 $A$ 可以相似对角化，当且仅当 $A$ 有 $n$ 个线性无关的特征向量。

3、正交相似对角化

解题方法:1、求特征值 2、求基础解系 3、正交化 4、单位化

正交：两个向量垂直

对称矩阵：不同特征值对应的特征向量是正交的

施密特正交化:$a_1a_2$

$b_1 = a_1$，$b_2 = a_2 - \frac{[a_2, b_1]}{[b_1, b_1]} \cdot b_1$

单位化：除以其值即可

4、特征值的性质

①$\lambda_1 + \lambda_2 + \cdots + \lambda_n = a_{11} + a_{22} + \cdots + a_{nn} \quad \text{（矩阵的迹：trA）}$

②$\lambda_1 \cdot \lambda_2 \cdot \cdots \cdot \lambda_n = |A|$

③ 若 $A$ 的特征值为 $\lambda$，则：

二次型

1、二次型

二次型与二次型矩阵的关系

对于 n 元二次型 $f(x_1, x_2, \dots, x_n)$，其一般形式可表示为:$f = \sum_{i=1}^n \sum_{j=1}^n a_{ij}x_ix_j \quad (a_{ij} = a_{ji}$) 对应的二次型矩阵 A 是一个 n 阶对称矩阵（满足 $A^T = A$），其中：

• 主对角线元素 $a_{ii}$ 是$x_{i}^2$项的系数
• 非主对角线元素 $a_{ij} \ (i \neq j)$ 是$x_ix_j$ 项系数的一半,因为$x_ix_j$ 会被拆分为$a_{ij}x_ix_j + a_{ji}x_jx_i$，且$a_{ij} = a_{ji}$。

2、求正交变换、化标准型

步骤：1、二次型矩阵 2、求特征值 3、求基础解析 4、正交化 5、单位化

3、顺序主子式

通过其判断二次型是否正定

定义：取矩阵前 $k$ 行、前 $k$ 列构成的子式：

依次得到：

• $\Delta_1 = a_{11}$
• $\Delta_2 = \det \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}$
• $\Delta_3 = \det \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$
• … 直到 $\Delta_n = \det(A)$。

顺序主子式与正定性（西尔维斯特判别法）

对于对称矩阵 $A$，二次型 $x^T A x$ 正定性的判别方法：

• 正定 ⟺ 所有顺序主子式 $\Delta_1, \Delta_2, \dots, \Delta_n > 0$
• 负定 ⟺ 顺序主子式 $\Delta_1 < 0, \Delta_2 > 0, \Delta_3 < 0, \dots$（符号交替）

概率论

事件的运算及概率

事件的基本概念

• 随机试验：在相同条件下可以重复进行，结果不唯一且事先不确定。
• 样本空间 $\Omega$：试验所有可能结果的集合。
• 事件：样本空间的子集。

1. $A、B$独立 $A$,$\overline{B}$ 、 $\overline{A}$,$B$、 $\overline{A}$,$\overline{B}$ 也相互独立
2. 若$A、B、C$相互独立 ① 两两独立 ② $P(ABC) = P(A)P(B)P(C)$
3. 两两独立 $\neq$ $A、B、C$相互独立

① 德摩根律 口诀：长杠变短杠，开口换方向

$\overline{A \cup B} = \overline{A} \cap \overline{B} \quad \overline{A \cap B} = \overline{A} \cup \overline{B}$

② 加法公式

$P(A \cup B) = P(A) + P(B) - P(AB)$

$\begin{aligned}P(A \cup B \cup C) = &P(A) + P(B) + P(C)- P(AB) - P(AC) - P(BC)+ P(ABC) \end{aligned}$

③ 减法公式 $P(A - B) = P(A\overline{B}) = P(A) - P(AB)$

④ 对立事件 $P(\overline{A}) = 1 - P(A)$

⑤ 独立事件 $P(AB) = P(A) \cdot P(B)$

2、古典概型

$C_{n}^{1} = C_{n}^{n-1} = n$

$C_{n}^{m} = \frac{n \times (n-1) \times \cdots \times (n-m+1)}{m!} = \frac{n!}{m!(n-m)!}$

$n! = n \times (n-1) \times \cdots \times 1$

全概率公式、贝叶斯公式

1、条件概率、乘法公式

条件概率：$P(B|A)=\frac{P(AB)}{P(A)}$ $P(A|B)=\frac{P(AB)}{P(B)}$

乘法公式：$P(AB)=P(A)\cdot P(B|A) = P(B)\cdot P(A|B)$

2、全概率、贝叶斯公式

① 设 $A$ 为发生的事件

② 找出完备事件组 $B_i$

③写出： $P(B_i)$ 及 $P(A|B_i)$

④ $P(A)=\sum_{i=1}^{n} P(B_i)P(A|B_i)$(全概率公式)

贝叶斯（逆概）公式：

贝叶斯本质就一个条件概率公式 $P(A∣B)$，也就是在$B$事件发生的情况下，$A$事件发生的概率

⑤ $P(B_i|A)=\frac{P(B_i)P(A|B_i)}{P(A)}$

五种重要分布

1、离散型—— 二项分布

记作：$X\sim b(n,p)$
分布律：$P\{X=k\}=C_{n}^{k}p^{k}(1-p)^{n-k}$

2、离散型——泊松分布

记作：$X\sim π(λ)$

分布律：$P\{X = k\} = \frac{\lambda^{k}}{k!} e^{-\lambda} \quad (k = 0, 1, 2, \cdots)$

3、连续性——均匀分布

记作：$X \sim U(a, b)$

概率密度：$f(x) = \begin{cases} \frac{1}{b-a} & a < x < b \\ 0 & \text{其他} \end{cases}$

4、连续性——指数分布

记作：$X \sim E(\lambda)$

概率密度：$f(x) = \begin{cases} \lambda e^{-\lambda x} & x > 0 \\ 0 & \text{其他} \end{cases}$

5、连续性——正态分布

记作：$X \sim N(\mu, \sigma^{2})$

概率密度：$f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x - \mu)^{2}}{2\sigma^{2}}}$

大数定理与中心极限定理

若$X \sim B(n,p)$，则 $X$近似服从正态分布 $N(np, np(1 - p))$

大数定理：当样本数量 $n \to \infty$ 时，样本均值趋近于总体的数学期望

常见的大数定理形式

(1)切比雪夫大数定理

设随机变量 $X_1, X_2, \dots, X_n$ 独立同分布，且期望 $E[X_i] = \mu$，方差有限。 则对任意 $\varepsilon > 0$：

含义：样本均值与真实均值的差异超过 $\varepsilon$ 的概率会趋近于 0。

(2)辛钦大数定理（强大数定理的一种）

如果 $X_1, X_2, \dots$ 独立同分布，期望为 $\mu$，那么

含义：不仅在概率意义上，几乎所有的样本序列，长期平均值都会收敛到 $\mu$。

参数估计

1、矩估计

先求数学期望， 求反函数，将变量换为样本均值

2、最大似然估计

设样本为

它们独立同分布，概率密度函数（或概率质量函数）为

其中 $\theta$ 是未知参数。

• 似然函数（Likelihood function）：$$L(\theta) = \prod_{i=1}^{n} f(x_i; \theta)$$
  它表示“在参数取值为 $\theta$ 时，观察到当前样本的概率”。
• 最大似然估计（MLE）： 找到使似然函数最大的参数：$$\hat{\theta} = \arg\max_\theta L(\theta)$$

通常我们取对数（更方便计算）：

然后对 $\theta$ 求导，解方程 $\frac{\partial \ell(\theta)}{\partial \theta} = 0$，得到估计值。

最大似然估计就是找到一组参数，使得在这组参数下，样本出现的可能性最大。

离散数学

集合论基础

集合：由“元素”组成的整体。性质：无序性、相异性、确定性、任意性。

幂集：集合 $A$ 的所有子集组成的集合，$|P(A)| = 2^n$。

笛卡尔积：$A \times B = \{(a,b) | a \in A, b \in B\}$。

关系

二元关系：集合上的有序偶组成的子集。

等价关系：自反、对称、传递。

等价类：与某元素相关的所有元素集合。

偏序关系：自反、反对称、传递。

• 例：$(\mathbb{N}, \leq)$。
• 空关系：$A \times B$ 的子集 $\varnothing$。在非空集上：反自反、对称、反对称、传递，但非自反。

集合大小与函数

无限集比较大小：通过建立一一对应。例：整数集 $\mathbb{Z}$ 与偶数集等势。

函数：集合间的一种特殊关系。

一个 $x$ 只能对应一个 $y$。

单射：不同的输入对应不同的输出。 满射：值域 = 陪域。 双射：既单射又满射，一一对应。

代数系统

同构：同类型、等势、运算对应相同。 半群：结合律。 群：半群 + 单位元 + 逆元。 交换群（阿贝尔群）：群且运算可交换。

阿贝尔群是一个满足 交换律 的群。 具体来说，设 $G$ 是一个集合，定义了一个二元运算 $*$，如果满足以下条件，则称 $(G, *)$ 是一个 阿贝尔群：

1. 封闭性：对任意 $a, b \in G$，有 $a * b \in G$。
2. 结合律：对任意 $a, b, c \in G$，有 $(a * b) * c = a * (b * c)$。
3. 单位元存在：存在一个元素 $e \in G$，使得对所有 $a \in G$，都有 $a * e = e * a = a$。
4. 逆元存在：对每个 $a \in G$，存在 $a^{-1} \in G$，使得 $a * a^{-1} = a^{-1} * a = e$。
5. 交换律：对所有 $a, b \in G$，有 $a * b = b * a$。

如果一个群只满足前四条性质，就是群（Group）；如果再加上第 5 条，就成为阿贝尔群（Abelian group）。

格与布尔代数

格：满足交换律、结合律、吸收律。 有补格：每个元素都有补元。 布尔代数：有补分配格，满足交换律、分配律、同一律、互补律。

图论

完全图 $K_n$：任意两点间都有边。

竞赛图：$K_n$ 上加方向得到的有向图。

正则图：每个顶点度数相同。

哈密顿图：存在一次经过所有顶点的回路。

欧拉图：存在一次经过所有边的回路。

条件：无向图连通且所有顶点度为偶数。

欧拉回路

定义：图中经过 每条边且仅一次，并且回到起点的回路。

条件（无向图）：当且仅当图是 连通的，且所有顶点的度数都是 偶数。

条件（有向图）：当且仅当图是 强连通的，且所有顶点的入度 = 出度。

哈密顿回路

定义：图中经过 每个顶点且仅一次，并且回到起点的回路。

不要求经过所有的边，只要求所有的顶点都走一遍。

判定条件：哈密顿回路没有像欧拉回路那样的简单充要条件。

• Dirac 定理：若一个 $n(n \ge 3)$ 阶简单图中，所有顶点的度数 $\ge n/2$，则该图存在哈密顿回路。
• Ore 定理：若任意两个不相邻顶点的度数之和 $\ge n$，则该图存在哈密顿回路。

数理逻辑

命题：能判断真假的陈述句。 原子命题：不可分。 复合命题：由联结词组成。

常见联结词：

否定：¬，合取：∧，析取：∨，蕴涵：→，等价：↔